能伸亦能屈,但不脱离中庸之道
题目取的挺有感,事情却很简单,即对于一组数据,可以用直线/平面拟合(逼近)它们,也可以用曲线/曲面拟合。不过,这件事情也很复杂,因为需要弄清楚拟合的结果是不是足够的好。
在言归正传之前,需要回答一个问题:为什么要对数据进行拟合?回答这个问题很简单,因为人类总是想用简单的模型去概括繁杂的事物。看,这个问题的答案本身就是答案。
下面图中所示的数据是本文的主角,你要问它来自何方,我指着大海的方向……
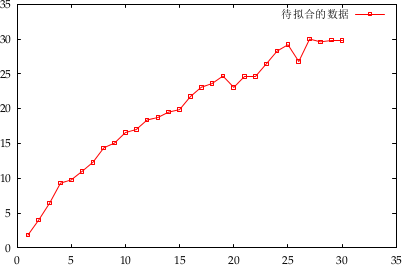
数据文件是 data.asc。
拟合方法与目标
大致有三种方法可以解决上面图中所示数据的直线与曲线的拟合问题。
第一种方法是非编程方法,即利用一些数据可视化工具读入数据,然后拟合,最后给出可视化的结果。本文使用的工具是 Gnuplot。
第二种方法是半编程方法,即调用现有的数值分析程序库中的黑箱函数完成数据拟合,然后给出拟合直线的参数、误差估计以及拟合优度。本文使用的程序库是 GSL。
第三种方法是全编程方法,即空手入白刃,在充分理解拟合原理的情况下,自己写出所有的代码来解决问题。这种做法,精神可嘉,但在一般情况下,特别是在第二种方法容易实现的情况下,不推荐这种做法。当然,理解拟合原理是非常有意义的。
感觉一篇文章中是很难将上述三种方法都讲述出来,况且此刻我对第三种方法还未有清晰的认识,所以暂时掘之为坑,只关注前两种方法。或许这样想会让我们轻松一下,不会炒菜,不意味不会品尝。
对于一组数据,无论是作直线/平面拟合,还是做曲线/曲面拟合,一个真正有用的拟合过程必须提供:(1) 拟合的参数;(2) 拟合所得参数的误差估计;(3) 拟合优度的统计度量。
如 果上述 (3) 中的结果表明了所拟合的模型与数据不一致,那么 (1) 与 (2) 中的结果通常没有多少意义。所以我们在使用既有的如 Gnuplot、GSL 这些工具或程序库进行数据拟合时,必须要对拟合优度有量化上的认识,而不能仅靠肉眼对拟合优度的定性观察。
Gnuplot 的直线与曲线的拟合
Gnuplot 对一组数据进行直线拟合的实现具体可围观下面的 Gnuplot 脚本:
# 设置将图形终端为 png 图像,输出 test.png 文件 set term png set output "test.png" # 设置图像标题 set title "Line fitting" # 直线表达式 f(x) = a * x + b # 给出待求参数的初值 a = 6.0; b = -4.0 # 直线迭代拟合 fit f(x) "km-sta-sample.asc" via a, b # 绘制数据与拟合的直线 plot f(x), "data.asc" using 1:2 with linespoints pointtype 4
设该脚本文件名为 test.gnu,使用以下命令输出 test.png 文件:
$ gnuplot test.gnu
所得 test.png 文件即下图,红色的直线拟合了绿色的数据点集。
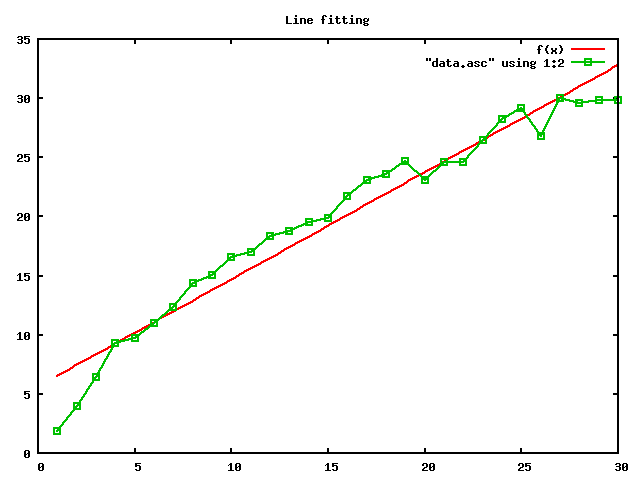
也许你的感觉一向不太敏锐,所以即使看到这条拟合的并不怎么好的直线也感觉不到它有什么不好。数据不说谎,所以我们需要对拟合直线的优度进行度量,而不能依靠我们经常犯错的双眼。下面,我们来看应该如何对这条直线的拟合优度进行度量。
当你在终端中在执行上述的 gnuplot 命令时,终端必定会输出类似以下的信息:
$ gnuplot km-plot.gnu
Iteration 0
WSSR : 4022.08 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 12.5731
initial set of free parameter values
a = 0.5
b = 1
/
Iteration 1
WSSR : 229.257 delta(WSSR)/WSSR : -16.544
delta(WSSR) : -3792.82 limit for stopping : 1e-05
lambda : 1.25731
resultant parameter values
a = 1.11079
b = 1.22798
/
Iteration 2
WSSR : 95.4978 delta(WSSR)/WSSR : -1.40065
delta(WSSR) : -133.759 limit for stopping : 1e-05
lambda : 0.125731
resultant parameter values
a = 0.94446
b = 4.81833
/
Iteration 3
WSSR : 90.9598 delta(WSSR)/WSSR : -0.0498896
delta(WSSR) : -4.53795 limit for stopping : 1e-05
lambda : 0.0125731
resultant parameter values
a = 0.905287
b = 5.61428
/
Iteration 4
WSSR : 90.9598 delta(WSSR)/WSSR : -2.45266e-07
delta(WSSR) : -2.23094e-05 limit for stopping : 1e-05
lambda : 0.00125731
resultant parameter values
a = 0.9052
b = 5.61605
After 4 iterations the fit converged.
final sum of squares of residuals : 90.9598
rel. change during last iteration : -2.45266e-07
degrees of freedom (FIT_NDF) : 28
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.80238
variance of residuals (reduced chisquare) = WSSR/ndf : 3.24857
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 0.9052 +/- 0.03802 (4.2%)
b = 5.61605 +/- 0.6749 (12.02%)
correlation matrix of the fit parameters:
a b
a 1.000
b -0.873 1.000
上述信息,从第 3 行至第 55 行显示的是直线拟合的迭代过程,这个迭代过程从我们初始给定的 a 与 b 的值开始,每一次迭代的目标是缩小 a 和 b 所确定的直线与数据点集的距离的统计量,即信息中的 WSSR 的值。可以看到,一共历经了 4 次迭代,WSSR 的值从大到小递减,第 3 次与第 4 次迭代所得的 WSSR 值相等,这意味着迭代过程收敛,直线拟合过程结束。
我们真正要关注的是第 57 行至第 76 行的信息。其中,第 68、69 行分别显示了计算出来的参数 a 与 b 的值以及它们的误差估计。前面我们说过,如果直线的拟合优度很差,那么所得 a 与 b 的值及其误差估计都没有太多的意义。
但是不幸的是 Gnuplot 并未进一步提供直线拟合优度的计算,它的 `help statistical_overview` 信息中如此说到(有所白话):为了估计所得参数的可信度,你需要使用拟合所得目标函数的最小值并结合卡方统计来确定用于量化拟合优度的卡方值,当然这需要更进一步的计算。
也就是说,Gnuplot 的开发者太懒了,将拟合过程进展到第 (2) 步便停止前进。那么,我们该肿么办?特别是我们还不是非常清楚拟合的原理,更对统计学中的这个分布那个分布一头雾水的时候,我们该肿么办?
其实这个问题很简单,只要我们怀着一颗勇敢又不求甚解的心。我们先不理睬鬼的卡方统计是什么,除非你的概率与统计学基础很不错。要计算直线的拟合优度,我们可以将 Gnuplot 所得的 WSSR 值与自由度的值代入下面的公式即可。
\[
Q = gammq\left(\frac{v}{2},\frac{WSSR}{2}\right)
\]
其中 WSSR 是迭代收敛后所得的最小的那个 WSSR 值,这个值在上面的 Gnuplot 输出信息的第 58 行给出了,那么 \(v\) 是什么?\(gammq\) 是什么?
\(v\) 就是自由度,就是我们要拟合的点数减去要待定的参数的数量。在本文的这个示例中,数据点数是 30,待定的参数是 2 个,所以自由度 \(v\) 为 28。实际上在上面的 Gnuplot 输出信息中的第 61 行已经给出了这个值。
\(gammq\) 是一个二元函数,这个函数可以给出一个概率值,即区间 \([0, 1]\) 内的值,这个值越大,表示直线的拟合优度越好。如果这个值大于 0.1,那么可以确信拟合的直线是足够好的;如果这个值大于 0.001,勉强可以接受;如果这个值小于 0.001,那么直线可能并不适合所给的数据点集,可以考虑更换为某种曲线模型。
现在,我不打算写出 \(gammq\) 函数的表达式,因为即使写出来,要编程实现这个函数也较为繁琐。有一个好消息,GSL 库中提供了这个函数的程序实现,即 gsl_cdf_chisq_Q 函数,它接受的两个参数与上面我们给出的 \(gammaq\) 的参数次序相反,即前者的第一个参数是 \(WSSR/2\),第二个参数是 \(v/2\)。利用 gsl_cdf_chisq_Q 函数,我们便可以写出一个计算直线拟合优度的程序,而且代码极为简单,围观一下:
#include <gsl/gsl_cdf.h>
#include <stdio.h>
int
main (void)
{
float v, x;
scanf ("%f %f", &v, &x);
printf ("%lf\n", gsl_cdf_chisq_Q (x/2.0, v/2.0));
return 0;
}
当然,要编译和运行这个程序,你需要安装 GSL 库。编译和运行这个程序的命令如下:
$ pkg-config --cflags --libs gsl | xargs gcc chisq-Q.c -o chisq-Q $ ./chisq-Q 28 90.95996 Q = 0.000034
我们将自由度 28 与 WSSR 值 90.95996 提交给 chisq-Q 程序后,它给出的直线拟合优度为 0.000034,这个值显然小于 0.001,所以我们可以确定这条直线并不适于拟合所给的数据点集。
当 然,我们说这条直线不适合所给的数据点集,主要指的是直线与点集的偏差太大,违背了我们进行数据拟合的初衷。但是有的时候,我们的目标就是要得到一条最能 逼近所给点集的直线,例如点集的 PCA 分析,在这样的情况中,我们只需要确定直线的参数,任务便可结束,无需确定拟合优度。也就是说,所得的拟合结果是否适合所给的数据点集,这主要取决于我们 的目的或需求。本文的目标显然指的是前者。
既然确定直线模型不适于拟合本文的数据点集,那么我们试试曲线模型可不可以。认真观察了一番数据,感觉它很像 \(f(x)=a\sqrt{x} + b\) 曲线,于是将前面的 test.gnu 脚本中的第 9 行修改为:
f(x) = a * x ** 0.5 + b
其中,** 是 Gnuplot 的求幂运算符。
然后再次运行 Gnuplot 命令,得到下面所示的数据与拟合曲线图:
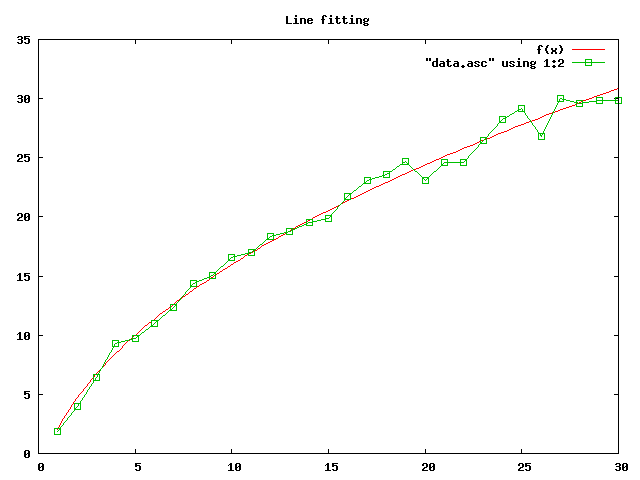
现在拟合的这条曲线对数据点集的贴近程度,即使不计算拟合优度,我们也可以确定的说它要比前面的直线拟合更好,但是本着客观科学的精神,我们还是让数据来说话。
先来看 Gnuplot 对这条曲线的迭代拟合过程终止后输出的信息:
After 4 iterations the fit converged.
final sum of squares of residuals : 16.9999
rel. change during last iteration : -2.81484e-10
degrees of freedom (FIT_NDF) : 28
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.779192
variance of residuals (reduced chisquare) = WSSR/ndf : 0.60714
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 6.43574 +/- 0.1146 (1.78%)
b = -4.39791 +/- 0.4511 (10.26%)
correlation matrix of the fit parameters:
a b
a 1.000
b -0.949 1.000
嗯,迭代次数依然是 4 次,收敛速度依然挺快。现在,将所得的自由度与 WSSR 最小值代入 \(gammaq\) 函数获取这条曲线的拟合优度:
$ ./chisq-Q 28 16.9999 Q = 0.861690
这次所得的拟合优度是 0.861690,显然远大于 0.1,这说明我们选择的这一曲线模型是可靠的。既然如此,那么所得到的参数 a 与 b 的值也是可靠的,它们的误差值也便有了意义。
如果你真的看了前面给出的 Gnuplot 两次的输出信息,也许会注意到输出信息的最后会有一个对角矩阵,例如:
correlation matrix of the fit parameters:
a b
a 1.000
b -0.949 1.000
这个矩阵是待定参数 a 与 b 的相关矩阵,非对角线上的数值表示 a 与 b 的相关度。这个值的符号为正,表示相关的两个参数值同号,本例即 a 与 b 同号,否则表示 a 与 b 异号。这个值的绝对值越大,即越接近 1,那么所得参数的误差估计也就越接近于真实误差。
不要问我为什么是这样,这些都是 Gnuplot 的帮助文档中说的。如果真要深究,其中的水很深。现在就可以唬你一下,Gnuplot 所采用的拟合算法是非线性最小二乘法中作为事实标准的 Levenberg-Marquardt 方法。也许以后我会慢慢的关注其中的道理,现在还是只关心直线或曲线的拟合所得参数值及拟合优度吧,而参数值的误差,也许只能作为不计算拟合优度时对拟合 质量的定性的判据。
GSL 直线拟合成功,曲线拟合未遂
在上一节中,我们已经用过一次 GSL 了。虽然还没有探索它的数据拟合功能,但是它的 \(gammaq\) 功能的具备给予了我们更多的信心,感觉它一定会做的比 Gnuplot 要好。
来,我们围观一下 GSL 中的直线拟合函数 gsl_fit_linear,其类型为:
/* 返回值为 0 表示函数运行成功,否则表示函数运行失败 */
int
gsl_fit_linear (const double *x, /* 数据点的横坐标值数组 */
const size_t xstride, /* 横坐标值数组索引步长 */
const double *y, /* 数据点的纵坐标值数组 */
const size_t ystride, /* 纵坐标值数组索引步长 */
size_t n, /* 数据点的数量 */
double *c0, /* 直线的截距 */
double *c1, /* 直线的斜率 */
double *cov00, /* c0 的误差 */
double *cov01, /* c1 的误差 */
double *cov11, /* c0 与 c1 的相关度 */
double *sumsq /* 等同于 Gnuplot 的 WSSR 值 */
);
由 gsl_fit_linear 函数的参数可知它只适用于直线模型 \(f(x)=c_0 + c_1 x\) 的拟合。
下面为 gsl_fit_linear 函数准备好每个参数。
前 5 个参数中,xstride 与 ystride 的值设为 1,表示数据点集 \(\{(x_i, y_i) |i=0, 1, \cdots, n-1\}\) 全部参与直线的拟合;剩下的三个参数需由一个自定义的从文件中读取数据的函数 input_points 产生,围观一下它的定义:
<定义读取点集文件的函数 input_points> =
static GList *
input_points (const gchar *filename)
{
GList *data_set = NULL;
GIOChannel * channel = g_io_channel_new_file (filename, "r", NULL);
GIOStatus status;
gchar *str, *strq, **data;
gsl_vector *v;
guint m, count = 0;
do {
status = g_io_channel_read_line (channel,
&str,
NULL,
NULL,
NULL);
if (!str)
continue;
strq = g_strstrip (str);
data = g_strsplit_set (strq, ";,\t ", 0);
for (m = 0; data[m] != NULL; m++);
if (m == 0)
continue;
v = gsl_vector_alloc (m);
for (gint i = 0; i < m; i++) {
v->data[i] = g_ascii_strtod (data[i], NULL);
}
data_set = g_list_append (data_set, v);
g_free (str);
g_strfreev (data);
count ++;
} while (status == G_IO_STATUS_NORMAL);
g_io_channel_unref (channel);
return data_set;
}
原谅我为了提高 input_points 函数对点集数据文件解析的健壮性,在上述代码中使用了 GLib 库中的列表、IO 通道以及字符串处理函数。如果你对 GLib 不熟悉并且讨厌熟悉它,那么你只需要知道 input_points 函数的功能是:根据文件名读取相应的数据点集文件内容并逐行进行解析,将解析出来的点的坐标值保存至 GSL 向量并将后者存储于 GLib 列表中,最后返回该列表。
基于 input_points 函数返回的列表便可产生 gsl_fit_linear 函数的第 1、3、5 个参数,剩下的参数皆为待定值,将它们定义为局部变量然后直接取址传于 gsl_fit_linear 即可。下面便是 gsl_fit_linear 函数全部参数的准备、函数调用以及结果显示代码,请围观:
#include <glib.h> /* 提供了列表容器 */
#include <gsl/gsl_fit.h> /* 提供了 gsl_fit_linear 函数 */
#include <gsl/gsl_cdf.h> /* 提供了 gammaq 函数 */
#include <gsl/gsl_vector.h> /* 提供了向量结构 */
<定义读取点集文件的函数 input_points>
static void
destroy_data (gpointer data)
{
gsl_vector_free (data);
}
int
main (int argc, char **argv)
{
GList *data_set = input_points (argv[1]);
guint n = g_list_length (data_set);
gdouble *x = g_slice_alloc (n * sizeof(gdouble));
gdouble *y = g_slice_alloc (n * sizeof(gdouble));
/* 构造 gsl_fit_linear 的第 1、3、5 个参数值 */
guint i = 0;
for (GList *it = g_list_first (data_set);
it != NULL;
it = g_list_next (it)) {
gsl_vector *v = it->data;
x[i] = v->data[0];
y[i] = v->data[1];
i++;
}
/* 剩下的参数值 */
gdouble c0, c1, cov00, cov01, cov11, sumsq;
/* 直线拟合 */
gsl_fit_linear (x, 1, y, 1, n,
&c0, &c1, &cov00, &cov01, &cov11, &sumsq);
/* 结果显示 */
g_print ("f(x) = %f + %f * x\n", c0, c1);
g_print ("c0 standard error: %f\n", cov00);
g_print ("c1 standard error: %f\n", cov11);
g_print ("correlation of c0 and c1: %f\n", cov01);
g_print ("Q = %f\n", gsl_cdf_chisq_Q (sumsq / 2.0,
(n - 2) / 2.0));
/* 内存回收 */
g_slice_free1 (n * sizeof(gdouble), x);
g_slice_free1 (n * sizeof(gdouble), y);
g_list_free_full (data_set, destroy_data);
return 0;
}
将上述代码与更上面的 input_points 函数定义部分的代码合并为 fitting-line.c 程序源文件,编译这个文件的命令如下:
$ pkg-config --cflags --libs glib-2.0 gsl | xargs \ gcc -std=c99 fitting-line.c -o fitting-line
运行编译生成的程序 fitting-line:
$ ./fitting-line data.asc f(x) = 5.616049 + 0.905200 * x c0 standard error: 0.455546 c1 standard error: 0.001445 correlation of c0 and c1: -0.022404 Q = 0.000034
输出了 5 行信息。第 1 行信息是确定了参数 \(c_0\) 与 \(c_1\) 的直线解析式,显然所得结果与前面 Gnuplot 拟合的直线相同。第 2、3 行信息分别是参数 \(c_0\) 与 \(c_1\) 的拟合误差估计,第 4 行是参数的相关度,这些结果与 Gnuplot 的结果不同,这主要是因为 GSL 的直线拟合算法采用的是线性最小二乘法,Gnuplot 采用的是非线性最小二乘法,而本文所涉及的数据拟合皆为线性最小二乘问题,所以 Gnuplot 的拟合参数的误差估计及相关性度量并不准确。第 5 行是直线的拟合优度,显然它与 Gnuplot 所得的直线拟合优度相等。
GSL 与 Gnuplot 的直线拟合除了拟合参数的误差估计及相关度不相同之外,所拟合的直线解析式及拟合优度是相同的。这样看起来,GSL 除了提供 \(gammaq\) 函数的计算之外,也没有太多优势。这样认为也许是因为你还没有注意到 Gnuplot 在拟合直线时,需要用户对拟合参数设定初值,而 gsl_fit_linear 则不需要。这依然是因为 Gnuplot 的拟合算法是非线性最小二乘法导致的,因为非线性最小二乘问题必须进行迭代求解,既然是迭代,那必须要给出起点,而线性最小二乘问题通常只需求解一个线性方程组,这不需要迭代。
一定要注意,本文所说的线性与非线性,指的是待拟合的各个参数是线性组合还是非线性组合,而不是函数解析式中自变量的线性/非线性组合。
既然我们已经使用 GSL 一帆风顺的完成了直线的拟合,宜将剩勇追穷寇,一举攻克曲线 \(f(x)=a\sqrt{x} + b\) 的拟合。
GSL 为直线的拟合单独提供了函数,然后又为一般的线性最小二乘问题提供了一个通用的函数 gsl_multifit_linear,不知这是为何,不过也没有必要深究。相比之下,Gnuplot 非常懒惰,它将线性最小二乘问题视为非线性最小二乘问题的特殊形式,所以它选择了一种更通用的拟合算法——用这种算法去拟合直线,宛若宰牛刀杀鸡。
围观一下 gsl_multifit_linear 函数的类型:
int
gsl_multifit_linear (
/* 系数矩阵 */
const gsl_matrix * X,
/* 观测值 */
const gsl_vector * y,
/* 待拟合确定的参数 */
gsl_vector * c,
/* 协方差矩阵 */
gsl_matrix * cov,
/* 拟合曲线与数据点的优值函数最小值 */
double * chisq,
/* 线性方程组求解过程中的内部状态 */
gsl_multifit_linear_workspace * work
);
这个函数所接受的参数与 gsl_multifit_linear 函数相迥异。我们需要耐心的逐个考察,以求获取直观认识。但是现在必须要对线性最小二乘问题进行一些形式化的定义,否则用语言很难表达清楚。
线性最小二乘问题及求解方法
假设有一个函数 \(f(x)=\sum_{k=1}^Ma_kX_k(x)\),其中 \(X_k(x)\) 是关于 \(x\) 的任意函数,还有一个点集 \(\{(x_i,y_i)|i=1,2,\cdots\,N\}\),现在试图计算出使得以下目标函数取得最小值的参数集 \(\{a_k\}\),这就是线性最小二乘问题。
\[
\chi^2(a_1,a_2,\cdots,a_M) = \sum_{k=1}^N\left[y_i - \sum_{k=1}^Ma_kX_k(x_i)\right]^2
\]
以本文所拟合的曲线 \(f(x)=a_1 + a2\sqrt{x}\) 为例,上述的目标函数便可实例化为:
\[
\chi^2(a_1,a_2) = \sum_{k=1}^N\left[y_i - \left(a_1 + a_2\sqrt{x_i}\right)\right]^2
\]
上式的一般形式是 \(f(a_1, a_2)=c_1a_1^2 + c_2a_2^2 + c_3a_1a_2\),看出它是什么了没有?如果看不出来,那么我们将 \(a_1\) 与 \(a_2\) 分别替换为 \(x\) 与 \(y\),即:\(f(x, y)=c_1x^2 + c_2y^2 + c_3xy\)。嗯,这就是传说中的二次型,而且由于 \(\chi^2(a_1,a_2) \ge 0\),所以它是半正定二次型,具有一个最小值。
总而言之,无论参数集 \(\{a_k\}\) 包含多少个参数,它的最小二乘目标函数总是半正定的二次型,并且该函数具有最小值。我们只要按照函数最小值的计算方法对目标函数略动手脚,那么参数集 \(\{a_k\}\) 便几乎唾手可得。还是以二元的二次型 \(\chi^2(a_1,a_2)\) 为例,这个函数的最小值对应的位置必定是一阶偏导数为 0,即:
\[
\begin{array}{lcl}
0 & = & \frac{\partial{\chi^2(a_1,a_2)}}{\partial{a_1}} & = & -2\sum_{k=1}^N\left[y_i - \left(a_1 + a_2\sqrt{x_i}\right)\right]\\
0 & = & \frac{\partial{\chi^2(a_1,a_2)}}{\partial{a_2}} & = & -2\sum_{k=1}^N\left[y_i - \left(a_1 + a_2\sqrt{x_i}\right)\right]x_i
\end{array}
\]
两个未知数,两个线性方程,后事如何,你懂的……按照这一思路,即使是 M 个参数构成的参数集 \(\{a_k\}\),也只是求解 M 个线性方程的问题。
解线性方程组的方法有很多,但是能同时适应于非奇异与奇异线性方程组的求解方法是 SVD(奇异值分解)法。所谓非奇异线性方程组指的是其中任何一个方程不是其他方程的线性组合或近似线性组合,否则就是奇异线性方程组。求解非奇异线性方 程组的方法主要有高斯消去法或 LU 分解法。这两种方法对于奇异线性方程组的求解会出现机器舍入误差积累从而导致求解结果往往与真实解相差甚远,这种情况下,SVD 法便散发出耀眼的光芒。
所 谓 SVD,就是将任意一个 \(M\times N\) 的矩阵 \({\bf A}\)——其行数 \(M\) 大于或等于列数 \(N\)——写成一个 \(M\times N\) 的列正交矩阵 \(\bf U\),一个 \(N\times N\) 的元素均为正数或零的对角矩阵 \({\bf W}\) 以及一个 \(N\times N\) 的正交矩阵 \({\bf V}\) 的转置矩阵的乘积形式,即:
\[
{\bf A}={\bf U}\times {\bf W}\times {\bf V}^T
\]
对一个矩阵搞此等分解,其意何为?且看下式:
\[
{\bf A}\times {\bf x} = {\bf b}
\]
其中,\({\bf x}\) 与 \({\bf b}\) 均为列向量。显然,这个公式表示的是线性方程组的一般形式。假设已对矩阵 \({\bf A}\) 进行了奇异值分解,那么上式便可写为:
\[
{\bf x} = {\bf A}^{-1}{\bf b} = {\bf V} \times {\bf W}^T \times {\bf U}^T\times {\bf b}
\]
之所以可以写成这样,是因为 \({\bf W}\) 与 \({\bf V}^T\) 都是列正交矩阵,它们的逆矩阵分别是它们的转置矩阵。也就是说对矩阵 \({\bf A}\)进行奇异值分解,方便计算它的逆矩阵。
有关奇异值分解与线性方程组求解的问题,水也是非常的深,我们暂时浮光掠影的围观一下即可。因为即使未能彻悟其中的道理,也可以无障碍的使用 GSL 所提供的奇异值分解函数的。
gsl_multifit_linear 函数正是使用 SVD 方法求解线性最小二乘拟合问题的。
现在可以揭晓上一节中 gsl_multifit_linear 函数的各项参数的含义了。它的前三项参数 X, y, c 即是构成线性方程组的矩阵与两个列向量,即:
\[
{\bf X}\times {\bf c} = {\bf y}
\]
其中,\({\bf X}\) 是 \(M\times M\) 的方阵,\({\bf c}\) 与 \({\bf y}\) 分别是 \(M\) 个分量的列向量。
第 4、5 项参数的含义与 gsl_fit_linear 函数中对应的参数相同,而第 6 项参数主要是用于在函数中保存矩阵 \({\bf X}\) 的奇异值分解结果的,诨号『工作空间』。
与 GSL 曲线拟合最后的搏斗
现在既知 gsl_multifit_linear 函数各项参数的含义,那么我们利用 GSL 直线拟合时所写的数据输入及 GSL 提供的工作空间准备函数,便可为 gsl_multifit_linear 函数准备好它需要的参数值。
首先围观如何产生矩阵 \({\bf X}\) 与向量 \({\bf y}\) 、\({\bf c}\)。由于要拟合的曲线是 \(f(x)=a_0 + a_1\sqrt{x}\),所以 M=2,而输入的点集包含 N 个点,那么矩阵 \({\bf X}\) 的规模是 NxM 的,向量 \({\bf y}\) 与 \({\bf c}\) 的分量数量也是 M,三个参数值的构造过程如下:
<输入点集并确定问题规模 M 与 N> =
GList *data_set = input_points (argv[1]);
guint N = g_list_length (data_set);
size_t M = 2;
<准备 gsl_multifit_linear 函数的前三个参数 X, y, c> =
gsl_matrix *X = gsl_matrix_alloc (N, M);
gsl_vector *y = gsl_vector_alloc (g_list_length (data_set));
GList *it = g_list_first (data_set);
for (guint i = 0; i < N; i++) {
gsl_vector *v = it->data;
gsl_matrix_set (X, i, 0, 1.0);
gsl_matrix_set (X, i, 1, pow (gsl_vector_get (v, 0), 0.5));
gsl_vector_set (y, i, gsl_vector_get (v, 1));
it = g_list_next (it);
}
gsl_vector *c = gsl_vector_alloc (M);
gsl_multifit_linear 函数的第 4、5 个参数值的构造如下:
<准备 gsl_multifit_linear 函数第 4、5 个参数值> =
gsl_matrix *cov = gsl_matrix_alloc (M, M);
gdouble chisq;
gsl_multifit_linear 函数第 6 个参数值是该函数的工作空间,为了防止疏忽而导致内存泄漏,通常是伴随曲线拟合临时分配,用完即销毁:
<工作空间构造、曲线拟合及工作空间销毁> =
gsl_multifit_linear_workspace *work = gsl_multifit_linear_alloc (N, M);
gsl_multifit_linear (X, y, c, cov, &chisq, work);
gsl_multifit_linear_free (work);
将上述步骤组合起来,并上结果的显示及内存回收的代码,全部过程如下:
#include <glib.h> /* 列表容器 */
#include <gsl/gsl_multifit.h> /* gsl_multifit_linear 函数 */
#include <gsl/gsl_cdf.h> /* gammaq 函数 */
#include <gsl/gsl_vector.h> /* 向量 */
#include <gsl/gsl_matrix.h> /* 矩阵 */
<定义读取点集文件的函数 input_points>
static void
destroy_data (gpointer data)
{
gsl_vector_free (data);
}
int
main (int argc, char **argv)
{
<输入点集并确定问题规模 M 与 N>
<准备 gsl_multifit_linear 函数的前三个参数 X, y, c>
<准备 gsl_multifit_linear 函数第 4、5 个参数值>
<工作空间构造、曲线拟合及工作空间销毁>
/* 结果显示 */
g_print ("f(x) = %f + %f * x ** 0.5\n", c->data[0], c->data[1]);
g_print ("Q = %f\n", gsl_cdf_chisq_Q (chisq / 2.0,
(N - 2) / 2.0));
/* 内存回收 */
gsl_matrix_free (X);
gsl_vector_free (y);
gsl_vector_free (c);
gsl_matrix_free (cov);
g_list_free_full (data_set, destroy_data);
return 0;
}
编译并运行这个程序:
$ pkg-config --cflags --libs glib-2.0 gsl | xargs \ gcc -std=c99 fitting-curve.c -o fitting-curve $ ./fitting-curve data.asc f(x) = -4.397906 + 6.435744 * x ** 0.5 Q = 0.861689
所得结果与 Gnuplot 的非线性拟合结果一致!
结语
我们赢了,欢呼……空虚……寂寞……发现前面还有更多的恶魔——最小二乘问题的数学模型、非线性拟合问题的求解方法、SVD 与线性方程组求解的关系等等——它们在等待着吞噬我们……继续前进,还是回家吃饭,这始终是个问题。
2021年4月04日 22:24
When you are browsing the internet in some cases I find a website which may be fairly thought invoking like this one. Delighted that I discovered your web blog as I greatly loved it and I look forward to the next article. An awesome website and i'll come back a lot more for more useful content… call conference ontario
2021年4月05日 05:56
I read this article. I think You put a lot of effort to create this article. I appreciate your work. Onewheel Accessories
2021年4月24日 19:41
I really appreciate this wonderful post that you have provided for us. I assure this would be beneficial for most of the people. Orlando Termite Control
2021年4月24日 19:59
I like to recommend exclusively fine plus efficient information and facts, hence notice it: Pest Control Orlando
2021年4月29日 20:19
Make the most of mainly premium substances - you will find him or her for: 발기부전
2021年5月04日 18:47
I understand this column. I realize You put a many of struggle to found this story. I admire your process. رقم مكافحة حشرات
2021年5月04日 18:56
I prefer merely excellent resources - you will see these people in: فني تكييف
2021年5月04日 19:03
Your texts on this subject are correct, see how I wrote this site is really very good. ستلايت
2021年5月04日 19:10
Acknowledges for penmanship such a worthy column, I stumbled beside your blog besides predict a handful advise. I want your tone of manuscript... تبديل بطارية السيارة امام المنزل
2021年5月04日 19:15
This is helpful, nonetheless it can be crucial so that you can check out the following website: تصليح طباخات الاحمدي مبارك الكبير
2021年5月21日 01:57
I came onto your blog while focusing just slightly submits. Nice strategy for next, I will be bookmarking at once seize your complete rises... 온라이바카라
2021年8月31日 08:01
jasapenerjemahbersumpah.com memberikan Anda layanan penerjemah tersumpah yang bisa menerjemahkan dokumen dokumen resmi untuk keperluan legal hukum. Jadi jika anda memerlukan bantuan penerjemah dokumen resmi anda bisa menghubungi jasa penerjemah tersumpah yang sudah mendapatkan sertifikat dari pemerintah. jasapenerjemahbersumpah.com . Rental Mobil Pamulang BSD mainnya Jakarta Anda transportasi untuk perjalanan di Tangerang ataupun Jawa Barat. Anda bisa menyewa mobil dari rental mobil Pamulang BSD Ini dengan harga yang lebih terjangkau. kendaraan yang disewakan sangat terawat dan juga diberi desinfektan untuk mencegah penularan penyakit. hubungi kami Jika anda ingin menggunakan jasa sewa mobil Pamulang di BSD Rental Mobil Pamulang BSD . cheap komodo tour package adalah paket perjalanan wisata yang ditawarkan dengan harga murah bagi Anda yang ingin menikmati perjalanan wisata di Pulau Komodo. paket perjalanan murah ini akan memberikan fasilitas-fasilitas yang lebih terjangkau namun masih memberikan kenyamanan untuk perjalanan wisata anda. cheap komodo tour package . Service AC Jakarta akan membantu Anda yang mengalami masalah AC di kota Jakarta. service AC di kota Jakarta ini bisa melayani pencucian AC, pengisian freon, dan perbaikan untuk berbagai kerusakan yang umum terjadi pada unit air conditioner. jasa service AC di Jakarta ini sudah sangat berpengalaman dan memberikan garansi hasil kerja. Service AC Jakarta . Jual Geotextile Woven dan non woven. geotekstil adalah lembaran garment yang biasanya dipergunakan untuk pembangunan beton ataupun aspal. Jika Anda membutuhkan produk geotekstil woven ataupun non woven maka anda bisa memesannya dari distributor produk geotekstil. pastikan anda memesan dari distributor resmi untuk mendapatkan produk geotekstil yang berkualitas. Jual Geotextile Woven . Aqiqah Terdekat memberikan Anda layanan aqiqah untuk putra-putri Anda. jasa aqiqah terdekat dari tempat tinggal Anda akan memberikan berbagai pilihan paket yang bisa anda sesuaikan dengan anggaran acara Aqiqah yang akan anda lakukan. di dalam syariat Islam sudah diatur tentang jumlah hewan yang akan dikorbankan untuk mengadakan acara Aqiqah. Anda bisa menanyakan segala sesuatu yang terkait mengenai pelaksanaan aqiqah ini kepada penyedia jasa aqiqah terdekat dari tempat tinggal Anda. Aqiqah Terdekat . Berita Maluku memberikan Anda update informasi terbaru tentang segala sesuatu yang terjadi di Maluku. berita Maluku dan Ambon ini akan memberikan informasi terkini tentang politik, hukum, pembangunan, dan segala sesuatu yang terjadi di sekitar Anda. Berita Maluku . Berita Maluku Tengah Yoga memberikan informasi yang terjadi pada kawasan Maluku Tengah. Anda bisa mengunjungi website resmi radio DMS untuk mendapatkan berita terbaru yang terjadi di Ambon Maluku. Berita Maluku Tengah . Jasa Fire Alarm memberikan Anda bantuan pemasangan fire Alarm System yang bisa mencegah kebakaran di gedung Anda. jasa fire Alarm System kami menyediakan konsultan untuk memastikan gedung Anda mendapatkan file Alarm System yang memenuhi ketentuan. Jasa Fire Alarm . digital marketing strategy adalah konsep pemasaran digital yang bisa membantu anda untuk mendapatkan penjualan. sebenarnya aplikasi dari Digital marketing ini sangat luas dan mencakup beberapa tools dan teknik. Oleh karena itu anda perlu meluangkan waktu untuk mempelajari dasar-dasar dari Digital marketing Jika Anda berniat memasarkan produk Anda secara online. digital marketing strategy . honeymoon Nusa Penida adalah paket bulan madu yang menyediakan perjalanan di Bali dan Nusa Penida. paket honeymoon Bali Nusa Penida ini juga mempunyai beberapa pilihan Hotel ataupun akomodasi yang bisa anda pilih. setiap akomodasi dan hotel ini memberikan penawaran harga yang berbeda. honeymoon Nusa Penida . Harga panel surya saat ini sudah semakin murah saya enggak ada banyak orang yang mulai berpikir untuk menggunakan panel tenaga surya ini. khususnya mereka yang tinggal di daerah-daerah pedalaman semakin tertarik untuk menggunakan panel tenaga surya karena lebih stabil untuk menghasilkan kebutuhan listrik mereka. ini adalah pilihan yang sangat efisien karena panel tenaga surya sebenarnya bisa bertahan hingga kisaran 25 tahun. jadi biasanya pengguna panel tenaga surya akan impas atau balik modal pada saat sudah menggunakan panel tenaga surya selama 5 tahun. Harga panel surya . web programmer lampung akan membantu anda untuk membuat website yang anda butuhkan. Jadi jika anda berada di Kota Lampung dan membutuhkan layanan pembuatan website anda bisa menghubungi web programmer Lampung. web programmer lampung . masyarakat semakin bermnat untuk belajar pemrograman. Karena semakin banyak hal yang bisa dibuat dengan bahasa pemrograman. Anda bisa membuat aplikasi ataupun website. ini bisa menjadi Jalan bagi orang-orang yang menguasai bahasa pemograman ini untuk mendapatkan penghasilan. masyarakat semakin bermnat untuk belajar pemrograman. . kursus programming Saat ini semakin diminati karena ada banyak orang yang tertarik untuk belajar bahasa pemrograman seperti CS, html, PHP dan sebagainya. bahasa pemrograman seperti ini akan sangat dibutuhkan di masa yang akan datang karena akan semakin banyak lagi software ataupun website yang dibuat. dengan menguasai bahasa pemrograman anda akan bisa mendapatkan berbagai jenis peluang untuk dikembangkan di masa depan. kursus programming . Channel perawatan kucing jalanan memberikan berbagai tips bagi Anda yang suka merawat kucing. Kucing adalah hewan yang saat ini menjadi hewan peliharaan paling favorit di Indonesia. namun kekurangan tahuan pemilik kucing biasanya membuat perawatannya tidak tepat. Channel perawatan kucing jalanan . paket backlink murah aman dan manual akan membantu anda untuk mendapatkan backlink yang berkualitas yang bisa anda gunakan untuk meningkatkan otoritas website anda dan menguasai berbagai kata kunci di hasil pencarian Google. tentunya Anda memerlukan paket backlink yang murah dan aman karena algoritma Google terus berkembang dari waktu ke waktu dan anda perlu memastikan bahwa kepentingan Anda terlihat alami. paket backlink murah aman dan manual . Kunjungi Youtube kami. ini adalah channel yang memberikan Anda pembelajaran tentang cara membuat website ataupun membuat catatan menjadi lebih populer. channel YouTube kepointernet ini bisa membantu anda untuk mendapatkan berbagai informasi yang bisa membantu perkembangan website Kunjungi Youtube .
2021年8月31日 08:03
cara ganti tema wordpress sangatlah mudah. anda bisa masuk ke dalam menu tampilan untuk mengubah tema dari website anda. untuk mengubah tema dari website WordPress anda sudah banyak sekali pilihan tema gratis yang bisa anda gunakan. namun jika anda memerlukan tema yang berkualitas Anda bisa membeli tema premium. cara ganti tema wordpress . Service laptop bandung bisa membantu anda untuk memperbaiki kerusakan laptop di kota Bandung. layanan service laptop yang profesional ini sudah mempunyai pengalaman yang sangat panjang dalam memperbaiki laptop. berbagai jenis kerusakan laptop bahkan Laptop mati total juga bisa diperbaiki oleh layanan service laptop di kota Bandung ini. Service laptop bandung . x-banner adalah banner yang mempunyai bentuk X. ini biasanya digunakan untuk alat promosi di depan toko. Jika anda ingin memesan X Banner untuk toko Anda maka anda bisa memesannya secara online dari jasa pembuatan banner. selain X Banner Anda juga bisa menggunakan y-banner. x-banner . roll up banner bagi Anda yang menginginkan kepraktisan Anda bisa memesan roll up banner. roll up banner ini menggunakan penggulung sehingga benar anda bisa dengan cepat dikemas dan dipasang di mana saja anda inginkan. untuk pembuatan roll up banner yang berkualitas anda bisa menghubungi jasa pembuatan banner berikut ini. roll up banner . dealer mitsubishi saat ini menyediakan berbagai pilihan kendaraan Mitsubishi terbaru. mulai dari xpander hingga Pajero. jika anda memerlukan mobil Mitsubishi di kota Jakarta Anda bisa mengunjungi dealer Mitsubishi Jakarta dan mendapatkan penawaran harga untuk mobil yang anda inginkan. dealer mitsubishi . hp 2 jutaan terbaik saat ini menjadi incaran banyak orang yang menginginkan HP dengan harga murah. HP di kisaran 2 jutaan Ini sebenarnya sudah mempunyai fitur yang cukup memadai untuk aktivitas-aktivitas kaum milenial. jika anda mencari hp dengan harga 2 jutaan Anda bisa mencoba berbagai keluaran terbaru dari merek HP berikut ini. hp 2 jutaan terbaik . hp gaming 1 jutaan terbaik adalah HP murah namun masih bisa anda gunakan untuk bermain game. tentu saja spesifikasi dari HP gaming 1 jutaan ini lebih difokuskan untuk bermain game namun belum bisa untuk menjalankan game-game yang memerlukan spesifikasi yang sangat tinggi. tapi bagi anda penggemar game game yang populer saat ini biasanya sudah bisa menggunakan HP 1 jutaan ini. hp gaming 1 jutaan terbaik . hp gaming 3 jutaan terbaik adalah HP yang bisa menjadi pilihan anda jika anda ingin bermain game yang spesifikasinya lebih tinggi. biasanya HP dengan kisaran harga 3jutaan ini sudah bisa menjalankan game-game yang paling berat saat ini. hp gaming 3 jutaan terbaik . Harga tenda membrane saat ini bisa ditentukan dari desain dan juga bahan yang Anda gunakan. untuk mendapatkan informasi lengkap tentang harga tenda ataupun kanopi membran ini anda bisa menghubungi kami. silakan kirimkan desain dari kanopi membran yang anda inginkan dan kami akan memberikan penawaran harga untuk tenda membran tersebut. Harga tenda membrane . aether BSD adalah kawasan perumahan di kawasan BSD yang sangat populer saat ini. Jadi jika anda mencari kawasan perumahan di BSD Tangerang Anda bisa mengunjungi kawasan ini. Perumahan aether BSD ini saat semakin populer dan banyak peminatnya. aether BSD . Agen sprei murah menyediakan Anda berbagai pilihan sprei dengan harga yang terjangkau. agen sprei kami mempunyai beberapa pilihan jenis kain sprei yang yang akan membuat tidur anda terasa lebih nyaman. jika Anda membutuhkan kain sprei dengan harga yang murah dalam jumlah besar anda bisa mengunjungi website distributor sprei murah kami. Agen sprei murah . zimbra mail server adalah sistem jaringan email perkantoran yang sangat populer saat ini. ada banyak perusahaan swasta dan juga instansi pemerintah yang menggunakan zimbra sebagai server mail pilihan mereka. hal itu dikarenakan zimbra juga sudah terintegrasi dengan berbagai sistem penjadwalan kerja. inilah yang membuat zimbra mail menjadi sangat diminati oleh banyak instansi zimbra mail server . Warehouse adalah layanan jasa yang bisa anda gunakan untuk menyimpan barang-barang anda. ada banyak sekali eksportir dan importir yang menggunakan layanan website ini untuk menyimpan barang-barang mereka. biasanya layanan ini juga ditawarkan oleh perusahaan logistik sebagai bagian dari paket layanan mereka. anda sebaiknya memilih layanan web host yang paling sesuai dengan barang yang akan anda Kirimkan. Warehouse . KAOS SERAGAM LENGAN PANJANG adalah kaos seragam yang mempunyai lengan panjang. biasanya kaos seragam olahraga lengan panjang ini digunakan oleh kaum muslimah untuk berolahraga. bahannya terbuat dari bahan yang sangat nyaman sehingga walaupun menggunakan lengan panjang tetap terasa adem. KAOS SERAGAM LENGAN PANJANG . GROSIR CELANA TRAINING juga memberikan bahan yang cepat mengeringkan keringat sehingga Anda tidak akan merasa lembab selama melakukan olahraga. jika anda memerlukan berbagai pilihan celana training Anda bisa melihat koleksi celana training yang kami tawarkan. grosir celana training kami bisa melayani pemesanan celana training dalam jumlah yang besar. jadi Anda bisa membuat setelan seragam olahraga untuk kantor anda ataupun komunitas anda. GROSIR CELANA TRAINING . money changer jakarta adalah layanan penukaran uang yang ada di kota Jakarta. jika anda mempunyai valuta asing atau mata uang asing yang ingin anda tukar kan Anda bisa mengunjungi money changer kami di Jakarta. kami juga menyediakan layanan money changer di Kota Lampung. layanan money changer Kami menggunakan harga kurs harian yang bisa anda pantau dari website kami. money changer jakarta . kabar trenggalek memberikan Anda informasi kabar berita tentang hal-hal terbaru yang terjadi di Kabupaten Trenggalek. Kabupaten Trenggalek saat ini sedang berbenah untuk memajukan perekonomian sehingga ada banyak sekali berita dan hal-hal terbaru yang terjadi di Kabupaten Trenggalek ini. Anda bisa mendapatkan info terbaru seputar Kabupaten Trenggalek dari website kami. kabar trenggalek . catering jogja adalah layanan catering yang menyediakan berbagai pilihan makanan favorit anda. catering Jogja juga menyediakan layanan nasi box atau nasi kotak yang bisa anda gunakan untuk acara-acara. untuk memesan paket catering Anda silakan mengunjungi website kami atau pun datang langsung ke alamat kami. jasa catering Jogja kami menyediakan berbagai pilihan menu yang bisa anda pilih Dan tambahkan sesukanya. catering jogja .
2021年8月31日 08:09
Pengrajin kayu saat ini membuat banyak sekali furnitur ataupun perlengkapan perlengkapan rumah tangga dari bahan kayu. ada banyak orang yang menyukai perlengkapan kayu ini karena mempunyai Nilai estetik. Anda bisa memesan dari pengrajin kayu ini untuk membuat talenan, piring,, sendok kayu dan masih banyak lagi kerajinan-kerajinan dari bahan kayu lainnya. ini akan membuat tampilan dari mebel ataupun furniture di rumah Anda terlihat lebih unik. pengrajin talenan kayu . bimbel pppk online dokter umum bisa membantu anda untuk mempersiapkan diri untuk menghadapi pppk dokter. materi bimbel dari pppk dokter ini sudah menggunakan materi terbaru yang saat ini diujikan pada saat ujian pppk dokter. Jadi anda akan siap menghadapi ujian pppk dokter dengan mengikuti materi pembelajaran di bimbel ini. bimbel pppk online dokter umum . bimbel pppk tenaga kesehatan juga tersedia di bengkel kami. kami mempunyai materi pppk tenaga kesehatan yang lengkap. materi pppk tenaga kesehatan ini akan membantu Anda mempersiapkan diri untuk menghadapi ujian pppk tenaga kesehatan terkini. bimbel pppk tenaga kesehatan . Jual APAR untuk gedung perkantoran ataupun rumah tinggal. Jika Anda membutuhkan alat bantu pemadam kebakaran atau yang biasa disebut APAR Anda bisa membelinya dari distributor alat bantu pemadam kebakaran. saat ini ada banyak sekali pilihan alat pemadam kebakaran yang bisa Anda persiapkan di kantor ataupun rumah Anda. alat pemadam kebakaran portable ini bisa menjadi pilihan darurat jika terjadi api di rumah anda. Jual APAR Jakarta . Saat ini ada banyak sekali agen travel yang menyediakan tiket perjalanan wisata dengan menggunakan berbagai alat transportasi. Jadi anda bisa dengan mudah menemukan agen travel yang menyewakan mobil ataupun motor untuk membantu kelancaran transportasi anda. Anda bahkan bisa menyewa bus pariwisata jika anda mempunyai rombongan dalam jumlah yang besar. Cari tahu informasi tentang agen perjalanan wisata terbaik di tempat yang anda tuju dengan menggunakan informasi berikut ini. Agen travel terdekat . Saat ini ada banyak orang yang mempunyai hobi untuk menulis dan mereka memerlukan tempat untuk menyalurkan hobi mereka itu. Oleh karena itu ada banyak website yang menyediakan sarana bagi mereka yang ingin meng online kan tulisannya. Anda sekarang bisa menulis cerita ataupun informasi lainnya dan mendapatkan penghasilan dari tulisan anda tersebut. menulis artikel dibayar . Cetak buku yang berkualitas namun dengan harga yang murah banyak dicari orang saat ini. Walaupun saat ini penggunaan buku cetak sudah semakin berkurang namun masih ada banyak sekali hal yang memerlukan jasa percetakan buku ataupun majalah. Biasanya perusahaan ataupun kampus masih merilis jurnal jurnal mereka dalam bentuk buku. Selain itu masih banyak lagi hal-hal yang memerlukan jasa percetakan buku yang berkualitas ini. Oleh karena itu masih ada banyak sekali orang yang menawarkan jasa percetakan buku dalam skala yang kecil hingga besar. cetak buku . Bisik bisik id adalah portal media berita yang saat ini semakin berkembang. Anda bisa mencari informasi atau berita-berita terbaru dari segala sesuatu yang terjadi baik di dunia maupun di indonesia dari portal bisik-bisik ini. Media berita nasional dan internasional ini akan membawa informasi baik itu olahraga, intertaiment, politik, hukum, dan lain sebagainya untuk menjadi bacaan sehari-hari anda. bisikbisik.id . Sedot wc mampet denpasar adalah layanan untuk menyedot septic tank yang sudah mampet. Bukan hanya untuk menyedot septic tank namun juga bisa membantu anda untuk mengatasi kemampetan pada saluran air apapun itu. Jasa sedot wc ataupun kuras wc mampet di bali ini sudah mempunyai peralatan yang sangat canggih sehingga bisa mengatasi mampet wc anda dengan waktu yang cepat dan bersih. Sedot Kuras Wc Mampet Denpasar Bali . Travel jakarta cirebon adalah layanan travel yang menyediakan transportasi bagi anda yang ingin berwisata dari jakarta ke cirebon. Selain menyediakan jasa travel dari jakarta dan cirebon ini anda juga bisa menggunakan jasa travel ini untuk melayani perjalanan anda menuju jogja, tegal, ataupun pekalongan. Layanan jasa travel kami mempunyai banyak sekali pilihan rute yang bisa anda sesuaikan dengan kebutuhan perjalanan anda. travel jogja pekalongan . Travel kediri surabaya juga melayani perjalanan antara kediri dan surabaya. Selain melayani perjalanan antara kediri dan surabaya travel kami juga melayani rute travel surabaya trenggalek. Anda bisa mengunjungi travel kami untuk mendaftarkan di jalanan anda ke daerah tujuan anda. travel surabaya trenggalek . Brio banjarmasin dengan simulasi kredit dan uang muka yang ringan bisa dapatkan disini. Kami adalah dealer ataupun sales honda banjarbaru dan banjarmasin. Anda bisa mendapatkan penawaran berbagai jenis mobil honda terbaru dengan harga yang terbaik dan cicilan yang yang paling sesuai dengan kebutuhan anda. Selain brio anda juga bisa membeli mobil crv dan juga mobil-mobil honda lainnya. Dealer mobil honda banjarmasin dan banjarbaru kami siap melayani pembelian mobil honda anda. Honda banjarbaru . Alat bantu pendengaran akan sangat membantu bagi anda yang mengalami gangguan pendengaran. Oleh karena itu anda perlu mencari alat bantu dengar yang mempunyai kualitas yang terbaik dan juga terjamin. Untuk itu anda harus membeli alat bantu dengar ini dari distributor yang terpercaya. Distributor alat bantu dengar yang resmi akan memberikan anda garansi untuk penggunaan alat bantu dengar dalam waktu yang lama. Jadi sekarang anda sudah bisa mendengar dengan lebih baik menggunakan alat bantu ini. alat bantu dengar . Nama aplikasi edit foto jadi anime saat ini banyak dicari oleh mereka yang ingin mengedit foto mereka menjadi anime. Bahkan banyak juga yang ingin membuat kartun menjadi lebih mudah dengan menggunakan aplikasi ini. Jika anda membutuhkan aplikasi pembuat anime ini anda bisa mendownloadnya dari google play store. Saat ini ada beberapa tool atau aplikasi yang bisa anda gunakan untuk membuat wajah anda menjadi warga anime. Apk edit foto jadi anime . Mebel jepara minimalis adalah mebel yang terbuat dari kayu jati dengan gaya desain yang minimalis. Jati jepara memang sudah karena terkenal kualitasnya sehingga ada banyak sekali orang yang berusaha untuk mendapatkan mebel ataupun furniture yang terbuat dari jati jepara ini. Terlebih lagi pengrajin mebel dan furniture jepara adalah pengrajin yang sudah sangat terampil sehingga hasil pekerjaan mereka pun sangat halus dan berkualitas. mebel jepara . Mebel jepara minimalis berkualitas bisa anda beli dalam berbagai bentuk furniture seperti tempat tidur tangga, meja makan, kursi, pintu, lemari, dan masih banyak lagi furniture lainnya. Mebel jepara yang terbuat dari kayu jati jepara ini akan menambah keindahan ruangan anda. pintu jati jepara . Jual pintu jati jepara murah juga bisa membantu anda untuk mendapatkan pintu rumah dengan tampilan yang mewah. Pintu rumah yang terbuat dari jati jepara ini tentunya mempunyai kualitas tampilan yang sangat baik sehingga anda bisa mendapatkan pintu jati jepara yang kuat dan tahan lama. Bagi anda yang ingin membeli pintu jati jepara ini silakan mengunjungi halaman website dari pengrajin pintu jati jepara. perabot jepara .
2021年8月31日 08:11
cara membuat website WordPress sangat mudah anda bisa mencari banyak panduan cara membuat website WordPress dengan menggunakan CMS ini. website WordPress dengan menggunakan CMS Ini adalah cara membuat website tanpa perlu menguasai bahasa coding sedikitpun. cara membuat website wordpress . paket honeymoon murah di Bali Bisa Anda gunakan jika Anda ingin menikmati hanimun di Bali dengan harga yang lebih murah. saat ini ada banyak sekali paket hanimun Bali yang ditawarkan dengan harga promo karena masa pandemi. paket honeymoon murah di Bali . harga paket honeymoon 3 hari 2 malam Bali saat ini lebih murah dari biasanya karena adanya masalah pandemi covid 19. jika anda tertarik untuk membeli paket honeymoon Bali ini anda bisa mengunjungi website website travel Bali yang menyediakan program bulan madu ataupun hanimun. biasanya pakai paket bulan madu ataupun hanimun ini ini ditawarkan dengan harga yang lebih terjangkau saat ini. harga paket honeymoon 3 hari 2 malam Bali . layanan sewa mobil terbaik di Bali memberikan Anda berbagai pilihan kendaraan ataupun mobil yang bisa anda Gunakan untuk transportasi Anda selama berlibur di Bali. jasa sewa mobil ataupun rental mobil di Bali ini sangat memperhatikan kebersihan kendaraan untuk mencegah penularan penyakit. Anda bisa menyewa layanan sewa mobil ini dengan harga yang lebih terjangkau. layanan sewa mobil terbaik di Bali . Jasa Adwords ada layanan yang bisa membantu anda untuk mengiklankan usaha anda di Google. Anda bisa mendapatkan pengunjung dengan menampilkan website anda di hasil pencarian Google secara berbayar. ada banyak orang yang ingin menggunakan Google adwords sini karena pengunjung yang datang adalah pengunjung yang memang sudah tertarik atau berminat untuk membeli produk yang ditawarkan. Jasa Adwords . Daftarpenyakit.info memberikan Anda pengetahuan tentang berbagai jenis penyakit beserta gejala dan pengobatannya. ini adalah pengetahuan yang sangat dibutuhkan beberapa saat ini karena hampir semua orang menjadi peduli dengan kesehatan mereka. Jika anda ingin mencari informasi yang lebih lengkap tentang berbagai jenis penyakit dan gejalanya Anda bisa mengunjungi website website info kesehatan seperti ini. Daftarpenyakit.info . Komodo Island Tour adalah paket wisata perjalanan Dimana anda akan menikmati liburan di Pulau Komodo. Komodo Island tour ini biasanya juga memberikan banyak pilihan paket yang bisa anda pilih. Anda bisa menyesuaikan rute perjalanan berdasarkan gaya wisata yang paling sesuai dengan anda. paket wisata ini sudah dilengkapi dengan akomodasi dan juga penginapan. Komodo Island Tour . Dana Darurat memberikan Anda berbagai solusi pada saat anda sedang membutuhkan bantuan keuangan. dana darurat ini biasanya anda sisihkan dalam rangka pengelolaan financial keuangan Anda. dana darurat ini biasanya akan sangat membantu jika tiba-tiba terjadi hal-hal yang diluar perencanaan finansial anda. Dana Darurat . Buku seribu mimpi adalah sebuah buku yang memberikan Anda panduan cara menafsirkan mimpi menurut kode-kode alam atau yang biasa juga kita kenal sebagai Primbon Jawa. ada banyak sekali buku tafsir mimpi yang saat ini populer dan sudah dituliskan kembali di berbagai website website. saat ini masih banyak orang yang mengunjungi website website tafsir mimpi ini jika mereka merasa gelisah dengan arti dari mimpi yang mereka dapatkan. Buku seribu mimpi . Try out SKB kesehatan Adakah sebuah ujian uji coba untuk mengetahui seberapa siap anda untuk mengikuti SKB kesehatan. beberapa lembaga pendidikan non formal sudah menyediakan berbagai pilihan pilihan materi try out atau uji coba ujian SKB kesehatan. ini bisa membantu anda untuk mendapatkan gambaran tentang bagaimana ujian sebenarnya sehingga Anda bisa menjadi lebih percaya diri untuk mengikuti ujian tersebut. Try out SKB kesehatan . crowdfunding indonesia bahasa Inggris adalah program investasi di mana Banyak orang bisa melakukan turunan untuk berinvestasi. program investasi crowdfunding ini akan menjadi terasa lebih ringan karena nilai investasi ditanggung secara bersama-sama. tentu saja nanti hasilnya pun harus dibagi bersama sama namun ini bisa menjadi solusi bagi Anda yang tidak mempunyai uang dalam jumlah besar untuk diinvestasikan. crowdfunding indonesia . jasa backlink adalah layanan pemasangan blackpink yang bisa membantu anda untuk mendapatkan otoritas nama domain yang sangat penting untuk menaikkan peringkat anda di hasil pencarian mesin pencari seperti Google. biasanya layanan jasa backlink akan memberikan berbagai pilihan paket yang bisa anda sesuaikan dengan tingkat persaingan kata kunci yang anda targetkan. jasa backlink . jasa backlink PBN permanen dan aman adalah program pemasangan jasa backlink yang memberikan pbn yang bisa membantu anda untuk mendapatkan backlink yang lebih relevan. jadi beking bukan hanya masalah otoritas saja tetapi juga masalah relevansi. dengan menggunakan backlink pbn Anda bisa mendapatkan faktor relevansi yang biasanya kurang bisa anda dapatkan dari hasil spam. jasa backlink PBN permanen dan aman . aswindra jaya layanan travel perjalanan wisata Bali yang bisa membantu anda untuk mendapatkan perjalanan wisata yang berkesan. agen perjalanan travel wisata Bali Jaya adalah agen perjalanan yang sudah sangat berpengalaman yang bisa membantu anda untuk mendapatkan pengalaman liburan terbaik di Pulau Bali. aswindra jaya . Paket wisata di Bali adalah paket wisata yang saat ini memang lagi berkurang peminatnya namun masih mempunyai potensi yang sangat besar di masa depan. Jika Anda berminat untuk mengikuti perjalanan wisata di Pulau Bali Maka sangat direkomendasikan untuk menggunakan paket wisata. paket wisata akan membuat perjalanan wisata anda menjadi bebas dari pikiran karena segala sesuatunya sudah dipersiapkan untuk anda. Paket wisata di Bali . jual tas karung adalah tas yang biasanya digunakan oleh jasa kurir untuk membawa barang-barang mereka ke mana-mana. tas karung memang mempunyai volume yang sangat besar sehingga bisa memuat banyak barang sekaligus Sehingga anda bisa membawa lebih banyak barang. tentunya anda ingin mendapatkan tas karung yang berkualitas baik dan tidak mudah rusak. untuk mendapatkan tas karung yang berkualitas baik ini anda bisa membelinya dari pabrik secara langsung. jual tas karung . jagoan kode saat ini ada banyak sekali aplikasi atau software yang dibuat dengan menggunakan kode kode bahasa pemrograman. Jika anda ingin belajar bahasa pemrograman atau belajar coding maka sebaiknya Anda mengunjungi website yang sudah mempunyai materi pembelajaran coding yang cukup lengkap. ini akan bisa membantu anda untuk mendapatkan keterampilan seorang programer. jagoan kode . Jasa Web akan sangat membantu bagi Anda yang ingin membuat website namun tidak menguasai bahasa pemrograman. jasa web Ini bisa memberikan Anda tampilan web yang anda inginkan. anda hanya perlu mendesain website tersebut secara sketsa dan memberitahukannya kepada web developer pilihan anda. seorang web developer biasanya kan bisa membuat tampilan website yang anda inginkan. Jasa Web .
2021年8月31日 08:12
Gamis Pria ada pilihan busana yang Islami untuk pria. biasanya ada banyak orang yang akan membeli gamis pria ini menjelang hari hari raya Islam. Mereka ingin mempergunakan baju gamis ini untuk bersilaturahmi ke rumah keluarga ataupun kerabat dan teman-teman mereka. jika anda tertarik untuk membeli baju gamis Islami yang berkualitas dan mempunyai desain yang baik anda saat ini sudah bisa membelinya secara online. Gamis Pria . Cetak majalah Saat ini semakin mudah dilakukan karena ada banyak sekali percetakan online yang bisa melayani pemesanan Anda. Anda bisa mengirim soft copy dari buku yang akan anda cetak ke percetakan ini. tanda sebaiknya berkonsultasi terlebih dahulu untuk mengetahui kualitas cetakan mereka dan juga biaya yang dibutuhkan. Cetak majalah . Mebel Jepara Murah adalah mebel yang sudah sangat terkenal akan kualitas nya. banyak sekali orang yang ingin membeli mebel jepara ini untuk menjadi ornamen di dalam rumah mereka. mebel jepara ini bisa saja menjadi pilihan bagi Anda yang menginginkan tampilan yang tradisional ataupun berkelah di dalam rumah anda. Mebel Jepara Murah . partisi movable wall adalah sistem pembagian ruangan yang bisa anda pasang dan lepas berkali-kali. dengan menggunakan partisi yang bisa dilepas ini maka anda mempunyai fleksibilitas untuk mengatur luas ruangan. saat ini ada berbagai tipe partisi ruangan yang bisa anda beli. ada yang menggunakan sistem geser dan ada juga yang menggunakan sistem lipat. partisi movable wall . tukang taman jakarta adalah layanan tukang yang bisa mengatur taman di rumah Anda ataupun di kantor anda. tukang taman sudah sangat berpengalaman sehingga bisa menata taman di rumah anda dengan tampilan yang terbaik. tukang taman bukan cuma sekedar menanam dan membersihkan namun juga bisa membentuk landscape taman yang terlihat indah dan profesional. tukang taman jakarta . Bisnis rumahan online adalah sebuah bisnis yang bisa Anda jalankan dari rumah Anda. di masa pandemi ini ada banyak sekali orang yang mencoba menjalankan bisnis rumahan untuk menambah penghasilan mereka. bisnis rumahan ini tentu saja menjadi sangat diminati karena bisa dilakukan tanpa perlu berkerumun dan membahayakan diri kita terkena penyakit. bagi Anda yang tertarik untuk mencoba bisnis rumahan saat ini sudah ada banyak sekali pilihan bisnis yang bisa Anda coba. Bisnis rumahan online . Jasa Pemasangan ACP Seven dan ACP akan sangat membantu meningkatkan tampilan dari gedung Anda. ada banyak sekali gedung yang menggunakan acp untuk membuat tampilan gedung mereka menjadi terlihat lebih artistik. memang bisa didesain dengan sesuka hati sehingga bisa memberikan tampilan gedung yang tradisional atau bahkan futuristik sesuai dengan keinginan pemilik gedung. Jika anda ingin membeli produk ini anda bisa memesannya secara online karena biasanya penyedia acp untuk gedung yang profesional ada di kota Jakarta. Jasa Pemasangan ACP Seven dan ACP Marks . update algoritma Google terbaru saat ini menjadi sangat dinamis dan membuat banyak pemilik website menjadi kaget. update algoritma ini mengakibatkan pergerakan peringkat atau rangking Di hasil pencarian Google yang sangat cepat. jika anda ingin mengetahui perkembangan algoritma Google yang terbaru sangat direkomendasikan bagi anda untuk selalu memantau perkembangannya. update algoritma Google terbaru . Pijat panggilan surabaya melayani pijat panggilan di wilayah Surabaya dan juga sekitarnya. pijat panggilan ini bisa membantu anda untuk menghilangkan rasa lelah akibat aktivitas seharian. namun jangan sampai menyangka bahwa ini adalah pijat plus-plus karena layanan pijat panggilan ini adalah profesional untuk membantu Anda meringankan rasa lelah di badan. Pijat panggilan surabaya . Pijat panggilan Makassar juga bisa anda gunakan selama 24 jam. Jadi anda bisa menghubungi layanan jasa pijat panggilan ini kapanpun anda merasa memerlukan bantuan pijat untuk menghilangkan rasa lelah anda. biasanya kaum profesional memang bisa bekerja hingga tengah malam sehingga Oleh karena itu ada banyak sekali jasa pijat panggilan baik di Makassar maupun di kota-kota lain yang melayani panggilan 24 jam. Pijat panggilan Makassar . Pijat panggilan semarang juga melayani 24jam Jadi jika anda merasakan kelelahan akibat bekerja di Kota Semarang Maka jangan ragu untuk menghubungi jasa pijat panggilan 24 jam kami. semua tenaga pijat yang dipekerjakan sudah mendapatkan training dan bisa bekerja dengan profesional. Pijat panggilan semarang . tips menjadi youtuber 2021 bisa membantu anda untuk mengembangkan channel Anda menjadi lebih populer. sebenarnya hal yang terpenting dari menjadi youtuber adalah kontinuitas atau rutin dalam melakukan upload video ke channel Anda. dengan rutin melakukan update video maka biasanya channel Anda akan mendapatkan reputasi yang terus berkembang dari waktu ke waktu. tips menjadi youtuber 2021 . frog channel adalah Chanel yang bisa memberikan Anda panduan untuk membuat origami ataupun menggambar. dari jika anda tertarik dengan aktivitas-aktivitas seperti pembuatan origami atau kerajinan tangan atau menggambar maka channel YouTube ini mempunyai konten yang sesuai untuk anda. frog channel . penerjemah tersumpah terpercaya adalah layanan penerjemah yang bisa membantu anda untuk menerjemahkan dokumen dokumen resmi. penerjemah tersumpah ini memang dipersiapkan secara khusus untuk menerjemahkan dokumen dokumen yang mempunyai kekuatan hukum dan memerlukan legalisasi dari berbagai instansi pemerintah yang terkait. penerjemah tersumpah terpercaya . cheat god of war 2 ps2 bisa anda dapatkan dari website ini. bagi anda games yang suka bermain game online Anda bisa mendownload banyak sekali game dari aplikasi yang disediakan oleh Android. tentu saja game game Android ini ada yang online dan ada juga yang offline Anda bisa mendownloadnya sesuai dengan tipe permainan yang anda butuhkan. cheat god of war 2 ps2 . karpet hotel adalah karpet yang dibuat secara khusus untuk Hotel. biasanya karpet ini mempunyai ukuran yang sangat besar dan memerlukan ruang penyimpanan yang sangat besar. Jika anda ingin memesan karpet hotel yang bisa anda gunakan untuk lobby ataupun ballroom maka sebaiknya Anda memesan karpet hotel tersebut dari distributor yang memang secara khusus menangani penyediaan karpet hotel. karpet hotel . paket wisata lombok memberikan berbagai pilihan paket perjalanan wisata di Pulau Lombok. ada banyak sekali tempat wisata yang menarik yang bisa anda kunjungi jika anda berwisata di Lombok. namun untuk membuat perjalanan Anda menjadi lebih terencana Maka sangat direkomendasikan agar anda menggunakan paket perjalanan wisata Pulau Lombok. paket perjalanan wisata Pulau Lombok ini sudah mencakup penginapan dan juga transportasi. paket wisata lombok . Kontraktor acp adalah layanan kontraktor yang bisa membantu anda melakukan pemasangan acp pada gedung Anda. yang disediakan oleh kontraktor acp ini menggunakan acp yang berkualitas tinggi dan tahan lama. anda bisa menentukan desain dari acp gedung anda atau meminta bantuan desainer untuk merancangkan acp yang terbaik untuk hidung Anda. acp ini sudah banyak sekali dipergunakan di gedung perkantoran untuk menambah ornamen pada gedung-gedung ini. Kontraktor acp .
2021年8月31日 08:33
jasapenerjemahbersumpah.com memberikan Anda layanan penerjemah tersumpah yang bisa menerjemahkan dokumen dokumen resmi untuk keperluan legal hukum. Jadi jika anda memerlukan bantuan penerjemah dokumen resmi anda bisa menghubungi jasa penerjemah tersumpah yang sudah mendapatkan sertifikat dari pemerintah. jasapenerjemahbersumpah.com . Rental Mobil Pamulang BSD mainnya Jakarta Anda transportasi untuk perjalanan di Tangerang ataupun Jawa Barat. Anda bisa menyewa mobil dari rental mobil Pamulang BSD Ini dengan harga yang lebih terjangkau. kendaraan yang disewakan sangat terawat dan juga diberi desinfektan untuk mencegah penularan penyakit. hubungi kami Jika anda ingin menggunakan jasa sewa mobil Pamulang di BSD Rental Mobil Pamulang BSD . cheap komodo tour package adalah paket perjalanan wisata yang ditawarkan dengan harga murah bagi Anda yang ingin menikmati perjalanan wisata di Pulau Komodo. paket perjalanan murah ini akan memberikan fasilitas-fasilitas yang lebih terjangkau namun masih memberikan kenyamanan untuk perjalanan wisata anda. cheap komodo tour package . Service AC Jakarta akan membantu Anda yang mengalami masalah AC di kota Jakarta. service AC di kota Jakarta ini bisa melayani pencucian AC, pengisian freon, dan perbaikan untuk berbagai kerusakan yang umum terjadi pada unit air conditioner. jasa service AC di Jakarta ini sudah sangat berpengalaman dan memberikan garansi hasil kerja. Service AC Jakarta . Jual Geotextile Woven dan non woven. geotekstil adalah lembaran garment yang biasanya dipergunakan untuk pembangunan beton ataupun aspal. Jika Anda membutuhkan produk geotekstil woven ataupun non woven maka anda bisa memesannya dari distributor produk geotekstil. pastikan anda memesan dari distributor resmi untuk mendapatkan produk geotekstil yang berkualitas. Jual Geotextile Woven . Aqiqah Terdekat memberikan Anda layanan aqiqah untuk putra-putri Anda. jasa aqiqah terdekat dari tempat tinggal Anda akan memberikan berbagai pilihan paket yang bisa anda sesuaikan dengan anggaran acara Aqiqah yang akan anda lakukan. di dalam syariat Islam sudah diatur tentang jumlah hewan yang akan dikorbankan untuk mengadakan acara Aqiqah. Anda bisa menanyakan segala sesuatu yang terkait mengenai pelaksanaan aqiqah ini kepada penyedia jasa aqiqah terdekat dari tempat tinggal Anda. Aqiqah Terdekat . Berita Maluku memberikan Anda update informasi terbaru tentang segala sesuatu yang terjadi di Maluku. berita Maluku dan Ambon ini akan memberikan informasi terkini tentang politik, hukum, pembangunan, dan segala sesuatu yang terjadi di sekitar Anda. Berita Maluku . Berita Maluku Tengah Yoga memberikan informasi yang terjadi pada kawasan Maluku Tengah. Anda bisa mengunjungi website resmi radio DMS untuk mendapatkan berita terbaru yang terjadi di Ambon Maluku. Berita Maluku Tengah . Jasa Fire Alarm memberikan Anda bantuan pemasangan fire Alarm System yang bisa mencegah kebakaran di gedung Anda. jasa fire Alarm System kami menyediakan konsultan untuk memastikan gedung Anda mendapatkan file Alarm System yang memenuhi ketentuan. Jasa Fire Alarm . digital marketing strategy adalah konsep pemasaran digital yang bisa membantu anda untuk mendapatkan penjualan. sebenarnya aplikasi dari Digital marketing ini sangat luas dan mencakup beberapa tools dan teknik. Oleh karena itu anda perlu meluangkan waktu untuk mempelajari dasar-dasar dari Digital marketing Jika Anda berniat memasarkan produk Anda secara online. digital marketing strategy . honeymoon Nusa Penida adalah paket bulan madu yang menyediakan perjalanan di Bali dan Nusa Penida. paket honeymoon Bali Nusa Penida ini juga mempunyai beberapa pilihan Hotel ataupun akomodasi yang bisa anda pilih. setiap akomodasi dan hotel ini memberikan penawaran harga yang berbeda. honeymoon Nusa Penida . Harga panel surya saat ini sudah semakin murah saya enggak ada banyak orang yang mulai berpikir untuk menggunakan panel tenaga surya ini. khususnya mereka yang tinggal di daerah-daerah pedalaman semakin tertarik untuk menggunakan panel tenaga surya karena lebih stabil untuk menghasilkan kebutuhan listrik mereka. ini adalah pilihan yang sangat efisien karena panel tenaga surya sebenarnya bisa bertahan hingga kisaran 25 tahun. jadi biasanya pengguna panel tenaga surya akan impas atau balik modal pada saat sudah menggunakan panel tenaga surya selama 5 tahun. Harga panel surya . web programmer lampung akan membantu anda untuk membuat website yang anda butuhkan. Jadi jika anda berada di Kota Lampung dan membutuhkan layanan pembuatan website anda bisa menghubungi web programmer Lampung. web programmer lampung . masyarakat semakin bermnat untuk belajar pemrograman. Karena semakin banyak hal yang bisa dibuat dengan bahasa pemrograman. Anda bisa membuat aplikasi ataupun website. ini bisa menjadi Jalan bagi orang-orang yang menguasai bahasa pemograman ini untuk mendapatkan penghasilan. masyarakat semakin bermnat untuk belajar pemrograman. . kursus programming Saat ini semakin diminati karena ada banyak orang yang tertarik untuk belajar bahasa pemrograman seperti CS, html, PHP dan sebagainya. bahasa pemrograman seperti ini akan sangat dibutuhkan di masa yang akan datang karena akan semakin banyak lagi software ataupun website yang dibuat. dengan menguasai bahasa pemrograman anda akan bisa mendapatkan berbagai jenis peluang untuk dikembangkan di masa depan. kursus programming . Channel perawatan kucing jalanan memberikan berbagai tips bagi Anda yang suka merawat kucing. Kucing adalah hewan yang saat ini menjadi hewan peliharaan paling favorit di Indonesia. namun kekurangan tahuan pemilik kucing biasanya membuat perawatannya tidak tepat. Channel perawatan kucing jalanan . paket backlink murah aman dan manual akan membantu anda untuk mendapatkan backlink yang berkualitas yang bisa anda gunakan untuk meningkatkan otoritas website anda dan menguasai berbagai kata kunci di hasil pencarian Google. tentunya Anda memerlukan paket backlink yang murah dan aman karena algoritma Google terus berkembang dari waktu ke waktu dan anda perlu memastikan bahwa kepentingan Anda terlihat alami. paket backlink murah aman dan manual . Kunjungi Youtube kami. ini adalah channel yang memberikan Anda pembelajaran tentang cara membuat website ataupun membuat catatan menjadi lebih populer. channel YouTube kepointernet ini bisa membantu anda untuk mendapatkan berbagai informasi yang bisa membantu perkembangan website Kunjungi Youtube .
2022年3月24日 00:08
Very interesting. https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html
2022年3月24日 00:09
interesting post. <a href="https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html">https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html</a>
2022年3月24日 00:10
Very interesting. [url=Very interesting. https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html]Very interesting. https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html[/url]
2022年3月24日 00:10
Sounds great. [url=https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html]https://www.propertymaintenance-gloucester.co.uk/flat-roof-repair-and-construction.html[/url]
2022年3月24日 00:12
Yes. [url=https://www.propertymaintenance-gloucester.co.uk/painter-and-decorator.html]
2022年3月24日 00:12
Great https://www.propertymaintenance-gloucester.co.uk/painter-and-decorator.html
2022年3月24日 20:11
This is totally great. www.treesurgeongloucester.com
2022年3月24日 20:12
Totally great. [url=[url=https://www.treesurgeongloucester.com/tree-surgeon-stroud.html][url=https://www.treesurgeongloucester.com/tree-surgeon-stroud.html]tree surgeon stroud[/url][/url]
2022年3月28日 23:15
k9 Doodie Patrol is the #1 pet dog waste removal company in New Jersey that provides the professional pooper scooper service also for communities & Parks. pooper scooper service
2022年3月28日 23:23
Red Oak Home Exteriors is Oklahoma's Affordable Choice for Custom Window installation services, Siding, Entry Door Installation, and Seamless Gutters. <a href="https://redoakhe.com/">home window replacement</a>
2022年3月28日 23:23
Red Oak Home Exteriors is Oklahoma's Affordable Choice for Custom Window installation services, Siding, Entry Door Installation, and Seamless Gutters. home window replacement
2022年8月10日 02:36
BSNL Personalized Ring Back Tone services, a mobile subscriber greet their callers with their favorite song as best choice, and this new My BSNL Tunes App service is an innovative service help the subscribers to express themselves, access information, entertainment and connect the other by greeting. BSNL Tune Most popular albums are vying for honor, but to find the best with codes or by names it is difficult, but now with this new launch of My BSNL Tunes App, each mobile user now have a chance to listen and activate their favorite songs of any language to set as BSNL caller tune on their mobiles.
2023年7月17日 22:09
Android Auto est une méthode courante pour connecter votre appareil Android au système d’infodivertissement de votre voiture informations diffusées et accéder à des fonctions telles que la navigation, la musique et la messagerie. meilleur adaptateur android auto sans fil Alors que de nombreux modèles de voitures plus récents incluent la prise en charge intégrée d’Android Auto, les véhicules plus anciens peuvent ne pas l’être. Les adaptateurs sans fil Android Auto peuvent vous aider.
2023年7月18日 19:17
TN newly Announce Tamil Nadu 5th Syllabus 2024, SCERT Tamil Nadu Board will Organise the 3rd Public Examinations in April 2024, 5th Exam will be based on the Syllabus Released by the State Council of Educational Research and Training Chennai is an Autonomous body of the Government of Tamil Nadu for Current Academic Session 2024, Every Year A Huge Number of Students Appeared for TNSCERT 5th Class Syllabus 2024 Should Check the new Syllabus Details here,All the Students who are Going to Appear for the Examination can make use of the Information Provided here and Accordingly practice Complete Tamil Nadu 5th,Syllabus 2024 given in order to give their best in the Examination.
2024年1月16日 14:48
The best article I came across a number of years, write something about it on this page
2024年1月25日 14:14
This post speaks volumes about the importance of gratitude and mindfulness. The reminder to appreciate the small joys in life is something we all need, especially in today's fast-paced world. Your words have inspired me to take a moment and reflect on the blessings around me. Kudos to you for spreading such a wonderful message!
2024年1月25日 14:38
Wow! Such an amazing and helpful post this is. I really really love it. It's so good and so awesome. I am just amazed. I hope that you continue to do your work like this in the future also.
2024年1月25日 14:53
Thanks for sharing the post.. parents are worlds best person in each lives of individual..they need or must succeed to sustain needs of the family.
2024年1月25日 15:04
I'm impressed, I must say. Very rarely do I come across a blog thats both informative and entertaining, and let me tell you, you ve hit the nail on the head. Your blog is important..
2024年1月25日 15:07
Discover the best selection and lowest prices on prescription and over-the-counter medications. Everything you'd expect from Canada's largest online pharmacy! CanadaCloudPharmacy.com is the most trusted name in high-quality, affordable medications, having been a first-class, certified online pharmacy serving many satisfied customers since 2001. In addition to discount prescription drugs, our Canada Pharmacy online provides a wide variety of discounted over-the-counter (OTC) medications, such as pain relievers, allergy medications, and even pet medications.
2024年1月25日 15:12
I feel very grateful that I read this. It is very helpful and very informative and I really learned a lot from it
2024年1月25日 15:18
Just admiring your work and wondering how you managed this blog so well. It’s so remarkable that I can't afford to not go through this valuable information whenever I surf the internet!
2024年1月25日 15:19
Decent data, profitable and phenomenal outline, as offer well done with smart thoughts and ideas, bunches of extraordinary data and motivation, both of which I require, on account of offer such an accommodating data her
2024年1月25日 15:28
This is often at the same time a good present that many of us seriously enjoyed browsing. It's not at all on a daily basis which i provide the likeliness to check something.
2024年1月25日 15:29
Nicely and effectively written blog and conveying the right information to the readers.Taxi in Alesund
2024年1月25日 15:34
This site is excellent and so is how the subject matter was explained. I also like some of the comments too. Looking forward to your next post.
2024年1月25日 15:40
Nicely and effectively written blog and conveying the right information to the readers.Taxi in Alesund
2024年1月25日 15:52
This post speaks volumes about the importance of gratitude and mindfulness. The reminder to appreciate the small joys in life is something we all need, especially in today's fast-paced world. Your words have inspired me to take a moment and reflect on the blessings around me. Kudos to you for spreading such a wonderful message!
2024年1月25日 16:00
Thanks for sharing the post.. parents are worlds best person in each lives of individual..they need or must succeed to sustain needs of the family.
2024年1月25日 16:07
Mendy has been playing for Real Madrid since 2019. This season, the defender has played 16 matches for the cream in all competitions, in which he scored one goal. The player's contract with the Madrid club is valid until the end of June 2025. The estimated cost of a football player, according to the Transfermarkt Internet portal, is € 20 million.
2024年1月25日 16:14
Normally, you can only use Payday for around 10,000 yen for the first time, but this plan is specialized for Apple products and has a significantly wider usage limit.
2024年1月25日 16:18
Thank you again for all the knowledge you distribute,Good post. I was very interested in the article, it's quite inspiring I should admit. I like visiting you site since I always come across interesting articles like this one.Great Job, I greatly appreciate that.Do Keep sharing! Regards,
2024年1月25日 16:24
Hello every one life is short live with joyness and dont loose your fashion life style visit online via american jacket store .com and hunt your choice out fit
2024年1月25日 16:29
Partaking in a particularly overpowering undertaking utilizes a great deal of our assets. Appreciation for sharing. I regard your site's facilities and strong data. Look at our site, and we will find you.
2024年1月25日 16:31
I will love the light for it shows me the way, yet I will endure the darkness because it shows me the stars.’
2024年1月25日 16:41
I recently came across your blog and have been reading along. I thought I would leave my first comment.
2024年1月25日 16:44
Spot up for this write-up, I honestly feel this fabulous website wants considerably more considerati
2024年1月25日 16:53
I definitely enjoying every little bit of it. It is a great website and nice share. I want to thank you. Good job! You guys do a great blog, and have some great contents. Keep up the good work.
2024年1月25日 17:08
Great to be here in your article or post, whatever, I figure I ought to likewise buckle down for my own site like I see some great and refreshed working in your site.
2024年1月25日 17:37
Just admiring your work and wondering how you managed this blog so well. It’s so remarkable that I can't afford to not go through this valuable information whenever I surf the internet!
2024年1月25日 17:38
I'm impressed, I must say. Very rarely do I come across a blog thats both informative and entertaining, and let me tell you, you ve hit the nail on the head. Your blog is important..
2024年1月25日 17:45
Thanks for sharing nice information with us. i like your post and all you share with us is uptodate and quite informative, i would like to bookmark the page so i can come here again to read you, as you have done a wonderful job.
2024年1月25日 17:55
Nicely and effectively written blog and conveying the right information to the readers.Taxi in Alesund
2024年1月25日 18:06
Thank you again for all the knowledge you distribute,Good post. I was very interested in the article, it's quite inspiring I should admit. I like visiting you site since I always come across interesting articles like this one.Great Job, I greatly appreciate that.Do Keep sharing! Regards,
2024年1月25日 18:12
I found your this post while searching for some related information on blog search...Its a good post..keep posting and update the information.
2024年1月25日 18:22
Thank you again for all the knowledge you distribute,Good post. I was very interested in the article, it's quite inspiring I should admit. I like visiting you site since I always come across interesting articles like this one.Great Job, I greatly appreciate that.Do Keep sharing! Regards,
2024年1月25日 18:22
At Bonehead Extracts Disposable, we’re committed to delivering the very best in quality and convenience. With our Bonehead Carts, you can experience the perfect blend of premium materials, carefully curated flavors, and hassle-free convenience. Choose The best Bonehead Extracts Bar for your next vaping experience, and discover the difference that quality and convenience can make.
2024年1月25日 18:28
Partaking in a particularly overpowering undertaking utilizes a great deal of our assets. Appreciation for sharing. I regard your site's facilities and strong data. Look at our site, and we will find you.
2024年1月25日 18:35
I recently came across your blog and have been reading along. I thought I would leave my first comment.
2024年1月25日 18:45
I recently came across your blog and have been reading along. I thought I would leave my first comment.
2024年2月22日 20:50
I like your post and also like your website because your website is very fast and everything in this website is good. Keep writing such informative posts. I have bookmark your website. Thanks for sharin
2024年11月12日 19:11
Very efficiently written information. It will be beneficial to anybody who utilizes it, including me. Keep up the good work. For sure i will check out more posts. This site seems to get a good amount of visitors. GB WhatsApp
2024年11月28日 19:08
This is a splendid website! I"m extremely content with the remarks!. csrd directive
2024年12月02日 21:24
My friend mentioned to me your blog, so I thought I’d read it for myself. Very interesting insights, will be back for more! eroina da fumare
2024年12月04日 20:21
Easily, the article is actually the best topic on this registry related issue. I fit in with your conclusions and will eagerly look forward to your next updates. container 10 fuß kaufen